2017运筹学复试真题回忆
一、、建立数学模型。
已知各个成分的混合百分比和费用,求建立线性规划模型,满足费用最低
二(此题数字有变动,大体是这样)、有甲乙丙三个城市,每年分别需要煤炭320,250,350万t,由A B 两个煤矿负责供应,已知煤矿年产量A为400万t,B为450万t,从两煤矿至各城市运价如下表所示,由于需求大雨产量,经过协商平衡,甲城市必要时可少供应0到30万t,乙城市需求量必须全部满足,丙城市需求量不得少于270万t,是求将甲乙两煤矿全部分配出去,满足上述条件又使总运费为最低的调运方案。
甲 | 乙 | 丙 | |
A | 15 | 18 | 22 |
B | 21 | 25 | 16 |
三、
四、.某厂使用A、B两种原料生产甲、乙、丙三种产品,有关数据见下表:
A B | 生产成本(万元/吨) | 销售价格(万元/吨) | |
甲 乙 丙 | 1.0 0.5 0.4 0.6 0.6 0.5 | 8 5 18 | 30 20 35 |
原料成本(万元/吨) | 5 7 | ||
原料可用数量(吨) | 350 460 | ||
(1)请写出使总销售利润最大的线性规划模型(其中甲、乙、丙产产量分别记为x1,x2,x3,约束依A,B原料次序):
(2)写出此问题的对偶规划模型
五、某服装厂制造大、中、小三种尺寸的防寒服,所用资源有尼龙绸、尼龙棉、劳动力和缝纫设备。缝制一件防寒服所需各种资源的数量如表(单位已适当给定)。不考虑固定费用,则每种防寒服售出一件所得利润分别为10、12、13元,可用资源分别为:尼龙绸1500米,尼龙棉1000米,劳动力4000,设备3000小时。此外,每种防寒服不管缝制多少件,只要做都要支付一定的固定费用:小号为100元,中号为150元,大号为200元。现欲制定一生产计划使获得的利润为最大,请写出其数学模型。
型号 资源 | 小 | 中 | 大 |
尼龙绸 | 1.6 | 1.8 | 1.9 |
尼龙棉 | 1.3 | 1.5 | 1.6 |
劳动力 | 4 | 4.5 | 5 |
缝纫设备 | 2.8 | 3.8 | 4.2 |
六、已知线性规划问题
max z = (c1+t1) x1+c2x2+c3x3+0x4+0x5
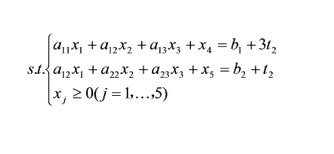
当t1=t2=0时,用单纯形法求得最终表如下:
X1 | X2 | X3 | X4 | X5 | |
X3 5/2 | 0 | 1/2 | 1 | 1/2 | 0 |
X4 5/2 | 1 | 1/2 | 0 | 1/6 | 1/3 |
Cj-Zj | 0 | 4 | 0 | 4 | 2 |
要求:1.确定c1,c2,c3,b1,b2,a11,a12,a13,a21,a22,a23的值;
2.当t2=0时,t1在什么范围内变化上述最优解不变;
