关于正交矩阵的部分知识,下边给出了正交矩阵的定义,(1)(2)是充要条件,当给出一个矩阵是正交矩阵的时候,要能立马反应出上述两个隐含的条件。

了解了正交矩阵的基本概念之后,我们还要了解正交矩阵的几何意义。首先,先来看一下向量的定义

要特别注意零向量,有多少个0取决于向量的维度。
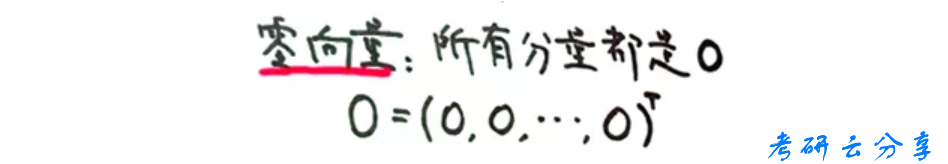
再有,需要注意两个向量相等的充要条件。
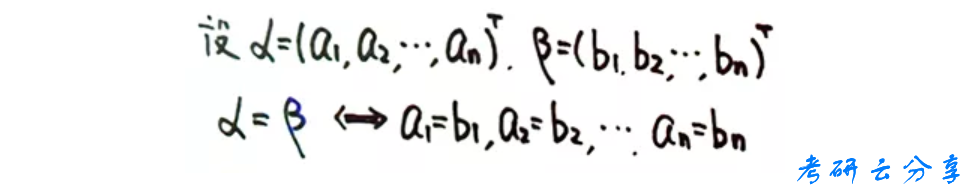
向量之间的运算有如下三大类

如果两个向量正交,那么它们一定是垂直的,则有例题如下

n维向量的长度怎么表示方式

好了目前有关向量的垂直的概念和长度的概念已经梳理完毕
那么开始带入到正交的问题中去

剩下的6个方程组情况类似就不再写出,观察上边的三个方程组,有如下三个特征
列向量坐标平方和为1,则一定为单位向量;
列向量内积为0则这两个列向量垂直;
每一个列向量都是单位向量,任何两个列向量都是垂直的;
好了,那么请判断下边的矩阵中哪个是正交矩阵?
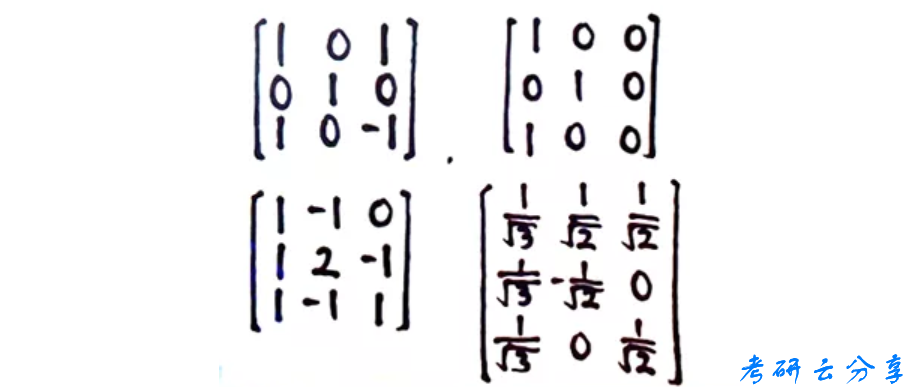
如果你真的找出了一个或者几个正交矩阵,那么恭喜你,需要把上边的知识点再复习一遍!
上图的错误最容易发生在大题求正交矩阵的时候,记得一定要单位化和正交化处理!
那么第一排第二个矩阵为什么不是正交矩阵?因为正交矩阵必是可逆矩阵,求出的正交矩阵如果行列式为0,则计算错误。

关于行列式为0的证明问题。
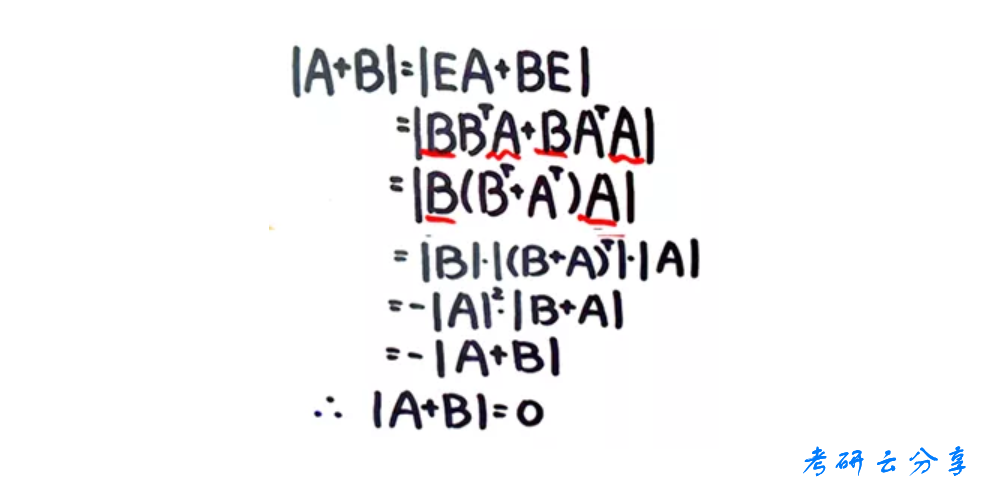
接下来进行向量章节,这一部分的的定理非常多也很容易发生混淆,所以一定要注意总结梳理,主要有如下几个大的部分。

这一章节主要的讲解步骤是在梳理完重要概念之后,先进行计算题的练习,再讲解分析小题和证明题。那么首先明确一下线性相关的定义

按照定义判别下述两题

接下来看一道填空题

由上述的过程可以看出把线性相关的问题转变成了齐次方程组有没有非零解的问题。
其实对于上述的小题而言,没有必要写上述的过程,可以直接写成下边的形式
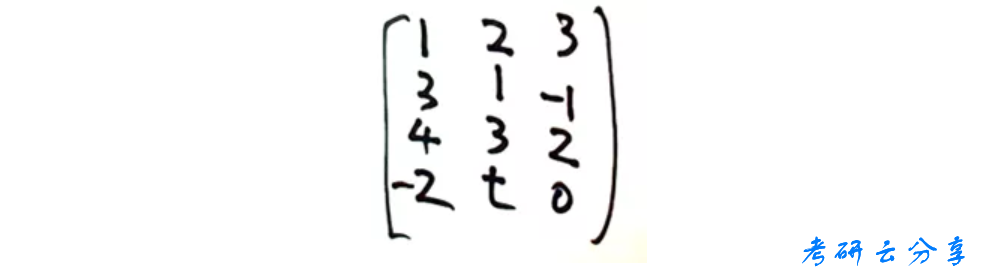
如果题目中给的是行向量也没关系,依旧直接把向量竖过来组成上述矩阵形式。
线性相关部分需要记住的几个重要定理如下

接下来我们看与之对应的线性无关的定义及题目。
证明向量线性无关的一大方法是定义法

要注意的两点
定义法证明必有系数都为0,使用恒等变形;
先做抽象假设,再由题目已知使用定义法证明。

上述问题主要在于找到要乘的矩阵是几次,只有根据题目的已知找到恰当的次数,才能方便我们证明。

证出k3=0后代回到公式(2)证明k2=0,继续回代到第一个式子得到k1=0,证毕。

特征值不同的特征向量线性无关,是一个重要定理,在线性代数的题目中经常会用到,请记牢!
最后看一道08年出过的真题

