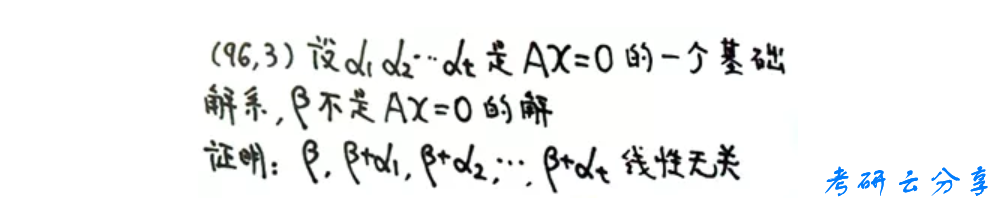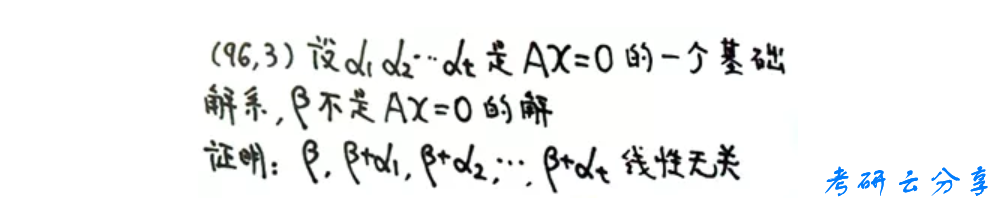
之前讲解了用定义法证明向量线性无关,今天要介绍的是第二种方法:用秩来证明线性无关。首先,先复习一下定义法的解题过程:

题目中的隐含条件要注意,例如本题的基础解系线性无关和上次笔记中提到的特征值不同的特征向量线性无关等。
在用秩做证明题和计算题之前,先看一下可能用到的知识点:
上边这道题之前用定义法求解过了,那么结合上边的知识点,换用秩的方法来解题:

通常来讲,用秩的方法求解这类问题会更简单。

定义法

总结:线性无关证明题有两种方法求解——定义和秩。
用定义来做,先抽象假设后恒等变形(有括号的要打开,可能要乘一项,一眼看出来直接乘或者乘完之后式子相加减)。

我们来看一下对上述充要条件的证明,之后就可以用这个条件来求解相对应的题目。

例题如下,选项中哪一组向量线性无关?

对于这类选择题,首先可以之间采用观察法,有的选项可以很直观地通过加加减减就能得出之间的线性关系。

对于CD两个选项采用观察法可能不能很快判断出来的时候,就要用到上边证明的结论,如果求出行列式等于零,则线性相关,否则,线性无关。
有关线性无关的证明就先告一段落,接下来也是线代部分很重要的一部分,证明题和计算题每年都会出现的知识——线性表示。还是先看一下有关定义和定理:
由定理对比上一部分知识,可以得出结论:线性相关和线性无关对应齐次方程组有没有非零解;线性表出对应非齐次方程组有没有解。


向量组之间的线性表出和等价的定义也要明确,不要与矩阵等价弄混!

举例如下:

证明两个矩阵等价的充要条件是证明它们的秩相等,而证明向量组等价是证明可以相互线性表出,所以二者没有关系,不要混淆!

那么定义和定理了解完之后,看一下具体的题目:




免责声明:本站所有的内容均来源于互联网采集或网友投稿提供,不能保证内容的真实性、完整性,仅供个人研究、交流学习使用,不涉及任何商业盈利目的。如果资料有误与官方发布不一致,请与官方最新发布为准,请联系本站管理员予以更改,如果涉及版权等问题,请联系本站管理员予以删除。
维权指引 |
权限说明 |
下载说明 |
内容投诉考研云分享 » 李永乐:线性代数强化直播课程第六次直播笔记整理