继续上次笔记，上次讲解的是通过概念解决线性表出的计算题和证明题，这次是关于一些线性相关的定理和用秩来解决相关问题。
子集相关则整体必是相关的，逆否命题：整体无关则子集也无关。
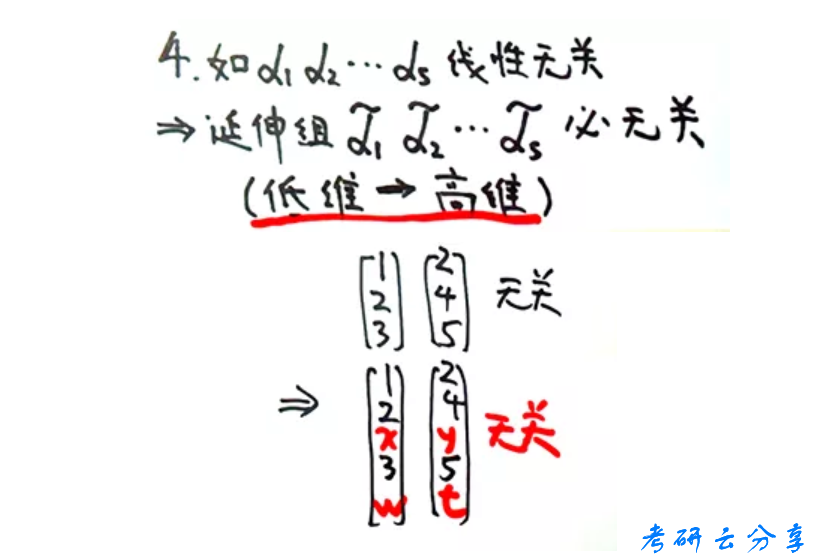
注意是充分非必要条件！同样找到它的逆否命题：
线性表出
与上述定理的区别在于，前边的是定性的，而对于此定理，假如有三个向量线性相关，不能得出任一个向量可由其他两个向量线性表出，为确定可以被线性表出的向量需要额外的条件。
以上就是部分用到的所有定理，接下来我们用例题来用定理。
首先来看第一问，我们用两种方法来解决：
第一种方法是用到上边的定理
第二种方法是通过概念
接下来第二问同样是两种不同的方法：反证法和秩。
一题多解在线代部分是很常见的，通过不同角度解决问题，能够锻炼我们对定理概念的灵活运用。
依旧是线性表出的问题，其实通过秩的方法来解决这类问题是比概念更加容易的，但是在有关秩的问题还未梳理完毕的情况下，我们再练习一下通过概念来证明线性表出：
现在对线性相关的问题做一下梳理总结，对相关的问题有如下的解决方案：
接下来就要进行很重要的一部分，关于向量组和矩阵秩的内容。
首先有关向量组的秩的部分，第一个重点知识：极大无关组。
通过上述定义要注意的是：一个向量组的极大线性无关组不唯一
通过证明得出结论，虽然向量组的极大无关组不唯一，但是不同极大无关组中向量的个数是相等的。
无关即秩等于S，反过来秩等于S就是无关。
再来看一道真题，这道题的正确率并没有很高，拿到这道题的时候你的解法会是什么？
直观的通过对已知条件的推论，用上述方法得出A是正确的。但是显然这种方法有些许绕。
我们直接看四个选项是比较向量组的个数多少，这时候要用到前边讲过的，很多同学都不熟悉的一个定理：
把条件和题目选项对应，则立马就可得A正确。在选出正确答案之后，能否试着举出反例来说明其他选项是错误的？
这道题是不是有些眼熟？前边的出现过，使用的解题方法是解方程组，计算量大，那么现在来看用秩怎么做：
