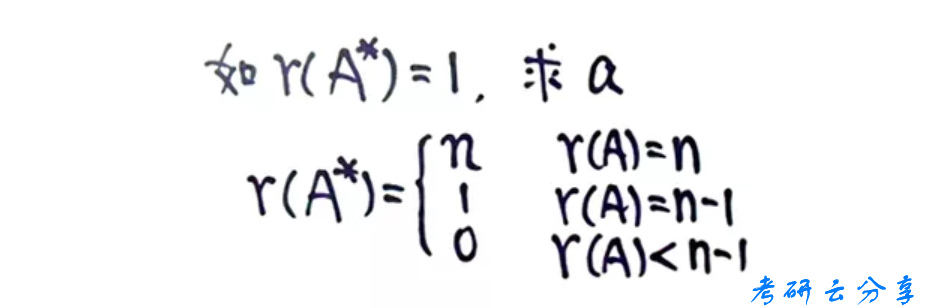这次笔记主要内容是矩阵的秩的概念、定理和真题解答
先来复习一下矩阵的秩定义：
在这个定理中，变换既可以行变换也可以列变换，当然也可以行列变换混用，秩都不变。
三者概念上不一样，第一个是矩阵的秩，后两个是向量组的秩，但是秩的数值大小是一样的。
定理3：
定理4：齐次方程组有非零解，则一定有无穷多解，其中线性无关的解向量的个数为n-r(A)。概念定理和基本公式梳理完之后，来看遇到题目的时候如何运用。遇到求解矩阵的秩的问题，通常有两种解法：一是经过初等变换秩不变，二是用行列式是否为零来讨论。此类型题目还经常与伴随矩阵的秩联系到一起，那么有关伴随和秩，需要记住下边的公式
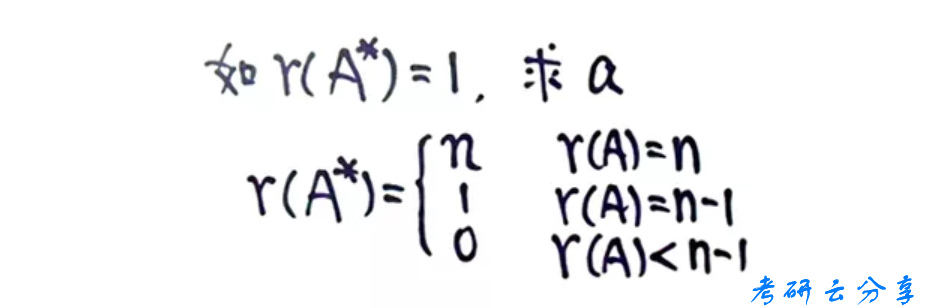
下面这种题目是结合了矩阵乘积为零和秩的问题，也是考研经常出现的一类题型，需要大家掌握。
A和B选项出现的结果是可能而不是绝对，所以正确答案是C。接下来我们看一下之前提到的一个公式的证明，要说明的是，对于此定义的证明方法有很多，这里只介绍一种大家可能不太习惯的方式。
下面一道08年的真题，正确率不是很高，在看证明之前，希望同学们可以自己试着做一做，要注意的是前边讲过的定理和公式的灵活运用！
接下来是一组证明结论对错的问题，复习一下之前线性相关的内容。
D选项是错的，上一次直播的笔记有过讲解，如果定理不熟悉，在选择题中可以自己举反例证明一下。
下面一道题是一道难点，很多同学因为思维定式选错，所以要仔细分析题目和解析哦！
首先排除C和D，因为题干只给了B是可逆矩阵，没有说A是否可逆。
AC的列向量可以互相线性表出，根据定义列向量组等价，所以选项B是正确的，可以举出反例证明A选项错误
本次到这里就结束了，下一次直播内容如下：
附件
李永乐：线性代数强化直播课程第八次直播笔记整理
下载文件
免责声明：本站所有的内容均来源于互联网采集或网友投稿提供，不能保证内容的真实性、完整性，仅供个人研究、交流学习使用，不涉及任何商业盈利目的。如果资料有误与官方发布不一致，请与官方最新发布为准，请联系本站管理员予以更改，如果涉及版权等问题，请联系本站管理员予以删除。
维权指引 |
权限说明 |
下载说明 |
内容投诉考研云分享 » 李永乐：线性代数强化直播课程第八次直播笔记整理
