这次开始进入到方程组部分,先来看齐次方程组的定义:

齐次方程组的解只有两种可能:零解和无穷多解,所以要关心有非零解的情况。

那么,有关齐次方程组的解,还需要掌握下边的基本性质和定理:

了解了解的性质,接下来是有关AX=0的基础解系的定义

那么同样的,证明基础解系也需要从三个方面来考虑

最后需要明确的一个重要概念:

那么概念定理之后我们需要用题目来介绍,如何求解基础解系。

由历年评分标准来看,上述的做法没有任何问题,但是中间的计算过程是不给分的。
意思就是化出行最简矩阵得2分,如果基础解系求错,最后也只得2分。
所以在考场上,如何直接快速地写出基础解系呢?
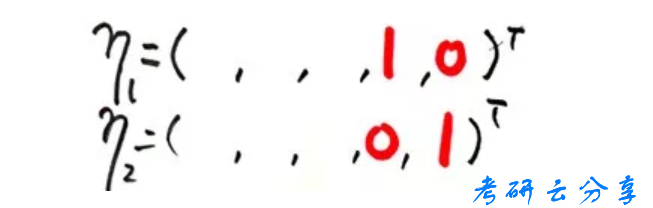
前边的数值为对应x4,x5的系数的相反数,按顺序填入解向量,既得到基础解系,如下图所示:

再看几个例子

然而有些题目,化出行最简的过程非常复杂,那么考虑化简到阶梯型然后代值求解。
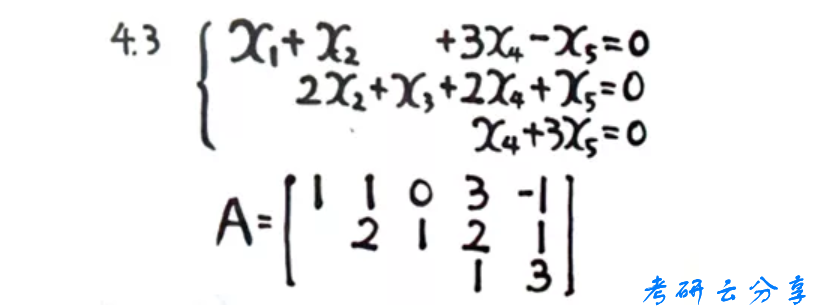
没有单位矩阵怎么选择自由变量?
原则:秩等于几就找不得零的几阶行列式,剩余的就是自由变量。
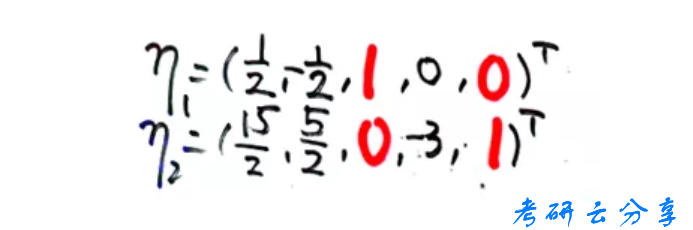
计算题的方法就是上述两种:化简成行最简或者阶梯型,那么来看一道选择题

首先,对于A选项,基础解系不存在是什么含义?就是齐次方程组只有零解。

更简单的一个方法,因为出现了伴随,所以可以考虑用伴随矩阵的秩的定义。

同样能得到和上述方法一样的结果,正确选项是B。

用伴随的秩的概念来解决基础解系的问题是很常见的,请大家一定要记牢。

对于含参的齐次方程组的求解,一定要注意讨论全所有可能的结果
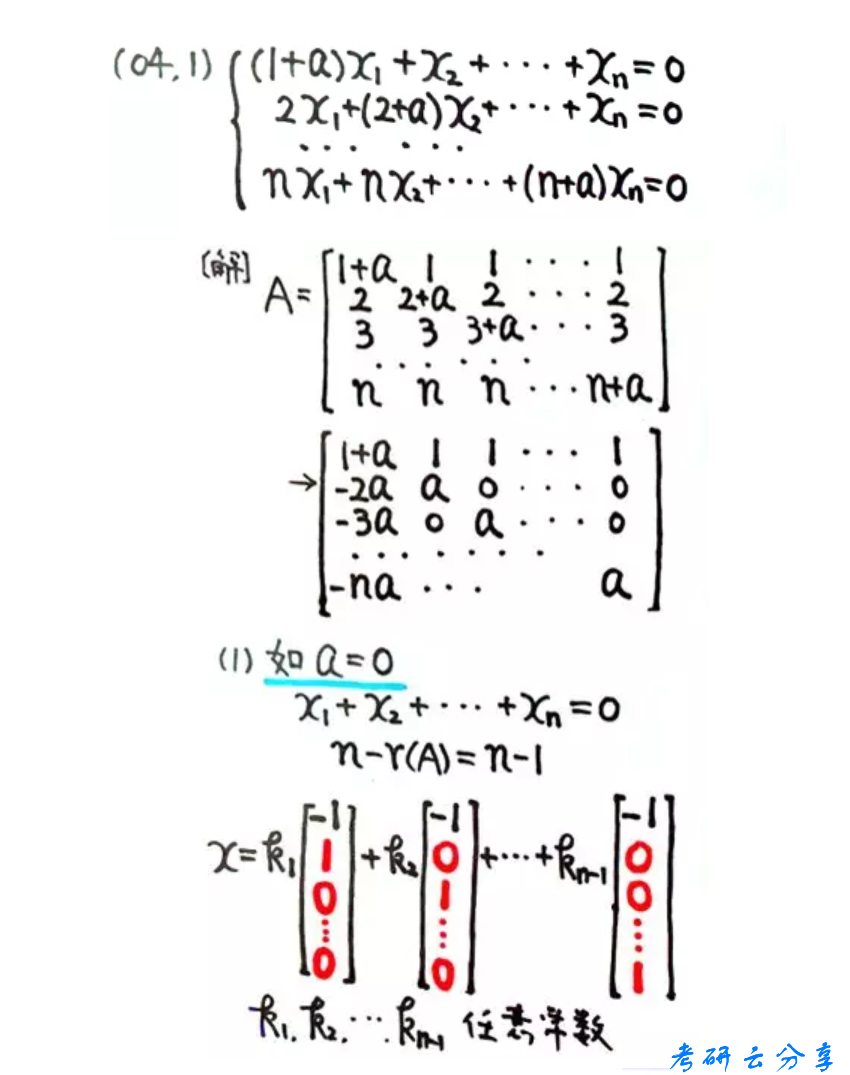
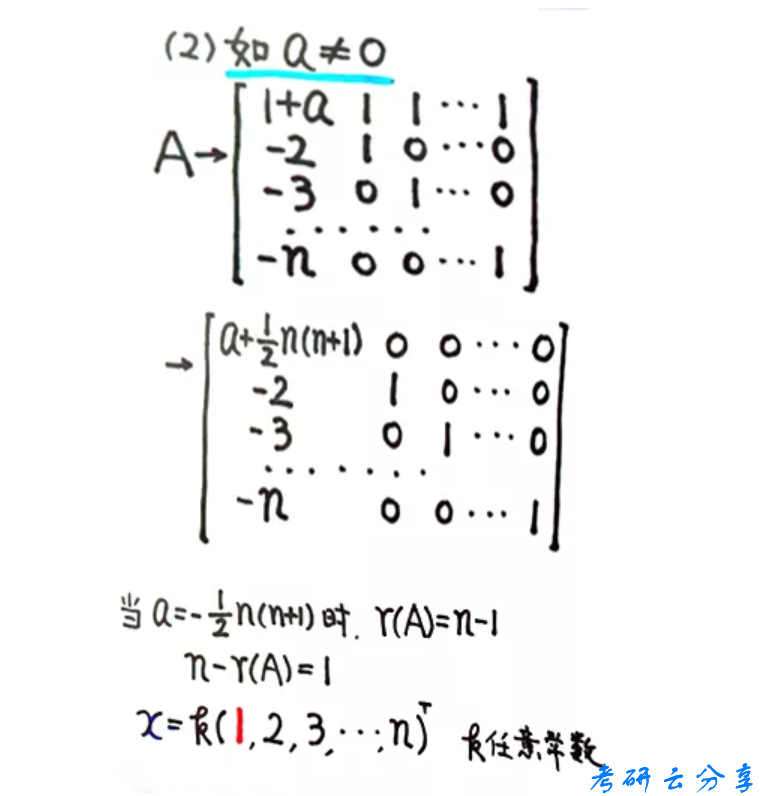
下面一题是19年数学一的真题,测试一下自己上边的知识是否已经都掌握了。

AB=0的考题在线代之前的内容中也曾多次出现,那么在齐次方程组的部分,相关的考点有:
r(A)+r(B)小于等于n;B的列向量是齐次方程组的解。

前边提到了证明基础解系的问题,那就请先思考一下下边的真题

分三个步骤来证明:先证是解,再证无关,最后说明是极大无关组。
具体过程如下:

接下来进行非齐次方程组的部分,首先看一下基本定义和概念。
非齐次方程组的解有三种可能:无解、唯一解和无穷多解。

结合之前讲过的一点性质,可以得到非齐次方程组的解的结构

与齐次方程组相同,求非齐次方程组的全部解的方法也是化简成行最简或者阶梯型
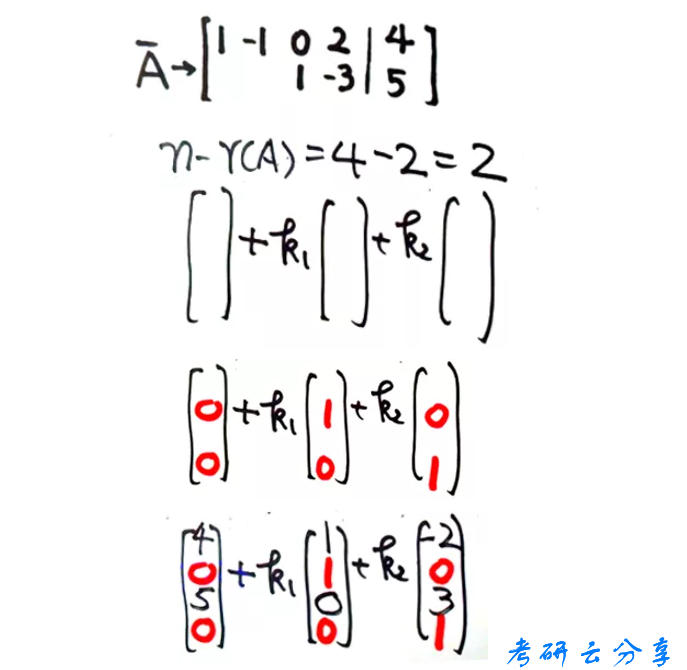
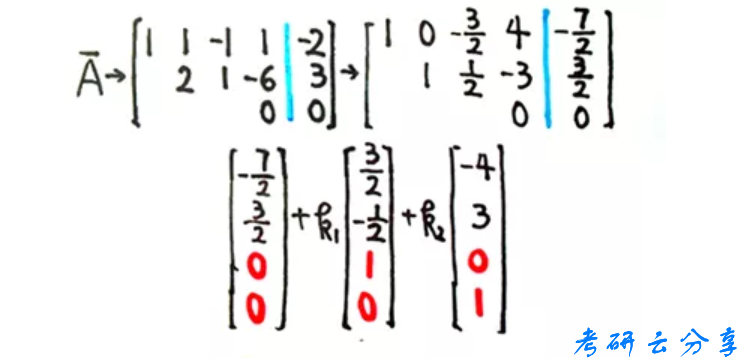
还可以不用化简到行最简,求得另一组较为简单的答案
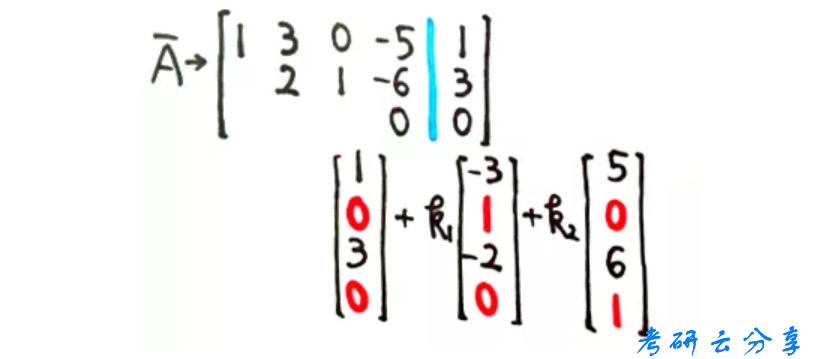
答案虽然不同,但都是正确的。



